M多くの研究室では、DC抵抗を測定するためのデジタル・マルチメータ(DMM)は十分に持っていますが、インダクタンス、キャパシタンス、インピーダンスの測定となると、LCRメータを見つけるのは容易ではありません。
LCRメータは、被測定デバイス(DUT)に交流電圧を印加し、その結果生じる電流を、交流電圧信号に対する振幅と位相の両方を測定します。容量性インピーダンスの場合、電圧波形の前に流波形が発生します。誘導性インピーダンスでは、電圧波形に遅れて電流波形が発生します。研究室にオシロスコープとファンクション・ジェネレータがあれば、同様の方法でさまざまな周波数のインピーダンス測定が行え、良い結果が得られます。この方法は、教育実験室の演習でも利用できます。
インピーダンスとは?
インピーダンスは、交流回路の電流の流れに対して正反対となります。抵抗(実数)とリアクタンス(虚数)の要素で構成され、通常、複素表記でZ = R + jX(R は抵抗、X はリアクタンス)と表します。
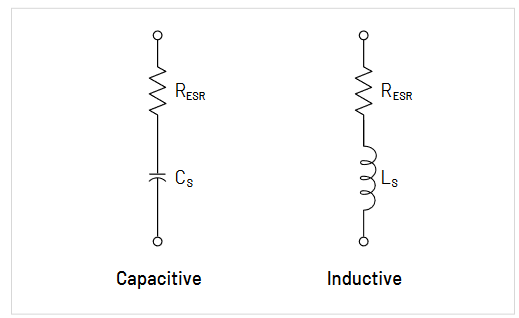
現実の部品は、電線、接続部、導体、誘電体などで構成されています。これらの要素が組み合わされて部品のインピーダンス特性が構成され、このインピーダンスは、テスト信号の周波数や電圧レベル、DCバイアス電圧や電流の有無、動作温度、高度などの環境要因によって変化します。これらの潜在的な影響のうち、テスト信号の周波数が最も大きな要因になることがあります。
理想的な部品とは異なり、現実の部品は純粋な誘導性や容量性ではありません。すべての部品には直列抵抗があり、これがインピーダンスのR成分です。しかし、リアクタンスのさまざまな要因にもなります。例えば、キャパシタには直列インダクタンスがあり、高周波になるとそれが顕著になります。実際のキャパシタを測定する場合、等価直列インダクタンス(ESL)はキャパシタンスの測定値に影響を及ぼしますが、それを独立した別の成分として測定することはできません。
インピーダンスの測定方法
このアプリケーション・ノートで説明するI-V法は、インピーダンス測定のための数ある方法のうちの一つに過ぎません。その他には、ブリッジ法、共振法があります。
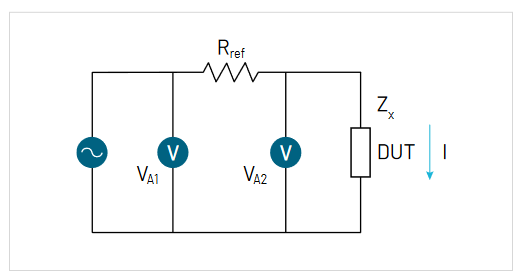
I-V法では、DUTの電圧と電流値を用いて、未知のインピーダンスZxを計算します。電流は、図2に示すようにDUTと直列に接続した精密抵抗の電圧降下を測定することで求めます。Zxの求め方を式1に示します。
式1:
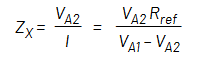
理論上の確度
このアプリケーション・ノートでは、オプションの任意波形/ファンクション・ジェネレータ(AFG)を装備した、テクトロニクスの2シリーズMSO(ミックスド・シグナル・オシロスコープ)を使用します。この2シリーズMSOは、信号の出力と測定の両方が行えます。内蔵しているAFGの周波数帯域は50MHzであり、この測定に最適です。オシロスコープのDCゲイン確度は3%です。式1で見るように、オシロスコープの電圧測定確度は、トータルのテスト確度において非常に重要な要素です。
式1によれば、この測定方法による理論上の確度は6%になります。
オシロスコープのサンプル・レートは、このテストで使用される出力信号の周波数よりもはるかに高いため、位相測定による誤差は無視できます。
インダクタンスとキャパシタンスの測定
オシロスコープとファンクション・ジェネレータを使用した、キャパシタ/インダクタ/等価直列抵抗(ESR)の測定について、以下の2つの例で紹介します。
使用機器:
- ファンクション・ジェネレータを内蔵した(Opt. 2-SOURCE)2シリーズMSO
- 1kΩの精密抵抗
- テストするキャパシタとインダクタ
- テクトロニクスのTPP0200型10:1電圧プローブ(2本)
このアプリケーションでは、テスト周波数が100kHz以下であるため、ほとんどのプロ仕様のオシロスコープとファンクション・ジェネレータを使用すれば、許容できる結果が得られます。例えば、テクトロニクスのAFG1000シリーズ、AFG2000シリーズは、入門レベルのプロ仕様のファンクション・ジェネレータであり、このアプリケーションでも十分に対応できます。
例1:10μFのセラミック・キャパシタ
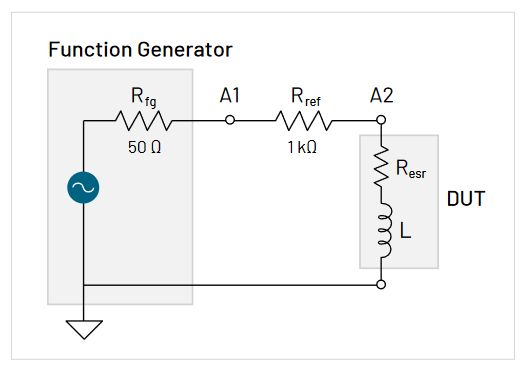
テスト回路をセットアップします(図3参照)。Resr とCは測定するセラミック・キャパシタのものであり、Rfg はファンクション・ジェネレータの50Ω出力インピーダンスです。
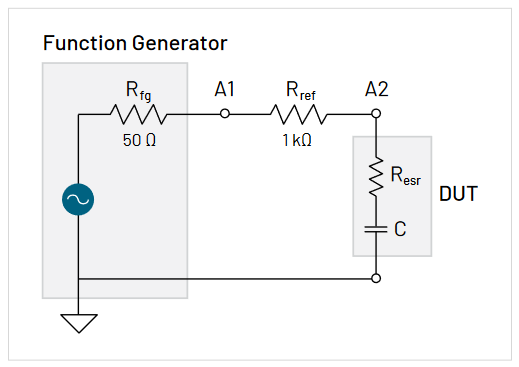
ファンクション・ジェネレータを、100Hzの正弦波、50Ωで1Vppの振幅を出力するように設定します。(測定は10MΩのプローブで行うため、オシロスコープによる電圧測定は、この振幅のほぼ2倍になります。)オシロスコープの垂直軸スケールを調整して、ディスプレイいっぱいに表示するようにします。レンジいっぱいに使用することで、電圧測定の確度が向上します。
図3のA1とA2を、オシロスコープでプロービングします。その波形を図4に示します。
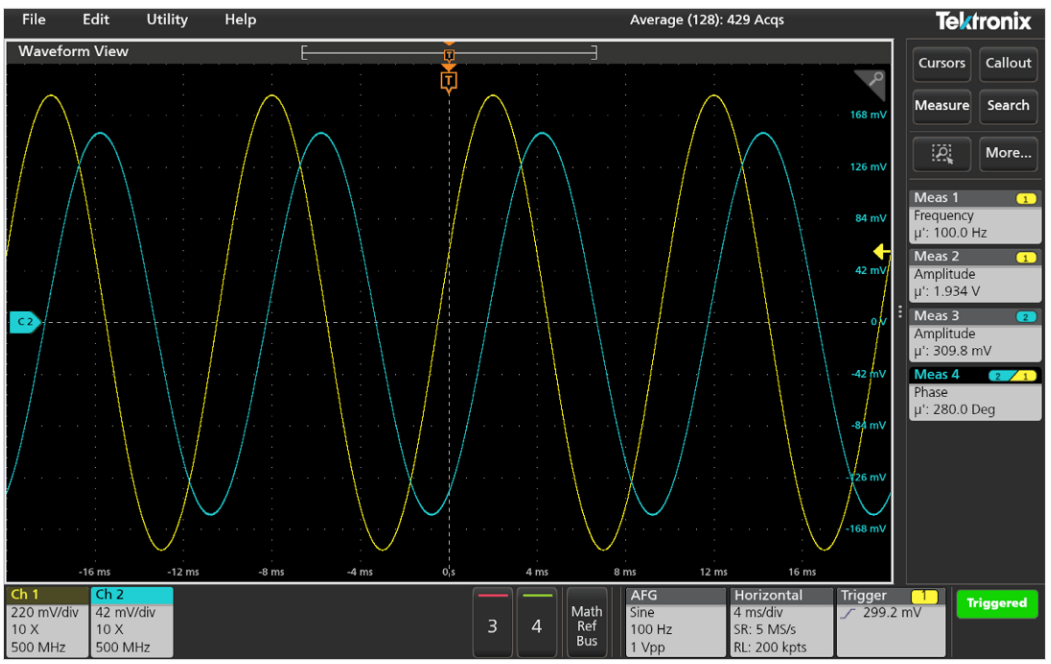
オシロスコープでアベレージ・モードを選択し、アベレージの回数を128に設定します。こうすることで、測定におけるランダム・ノイズを抑えることができます。オシロスコープを設定して、Ch1の周波数、Ch2とCh1間の位相、Ch1の振幅、Ch2の振幅を測定します(図4参照)。これらの値を記録します。
測定のセットアップは、以下の通りです。
出力周波数、f = 100Hz
精密抵抗、Rref = 1kΩ
オシロスコープによる測定から、以下の値が得られます(図4参照)。
A1における電圧振幅、VA1 = 1.934V
A2における電圧振幅、VA 2 = 0.310V
A2で測定した、A1に対する電圧の位相差、θ = 280.0° = –80.0°
ノードA1の電圧は試験回路全体の電圧降下、ノードA2は被測定キャパシタの電圧降下になります。直列RC回路の予想通り、キャパシタの電圧は回路全体の電圧に対して位相角θだけ遅れます。
被測定キャパシタのインピーダンスは、式1で求めることができます。
インピーダンスは極座標で表すことができ、その大きさは次の式で求められます。
式2:
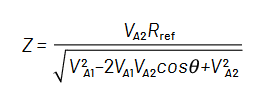
インピーダンスの角度は、2つの角度の引き算で求められます。
式3:
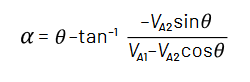
この例のテストでは、式2と式3を用いて、被測定キャパシタのインピーダンスの大きさと角度を求めることができます:

ここで、インピーダンスの直交形式に変換して、抵抗とキャパシタンスを求めることができます。
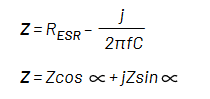
上記の式を用いて、DUTのESRとキャパシタンスを求めることができます。
式 4:
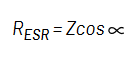
式 5:
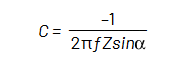
式4と式5から、被測定キャパシタのESRとキャパシタンスを計算することができます。
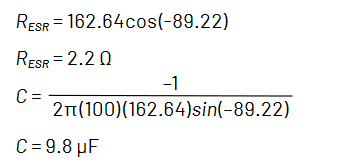
表1は、オシロスコープとファンクション・ジェネレータで得られた結果を、ローコストのVNAと従来のLCRメータによる結果と比較したものです。この例で使用したLCRメータは、一般的な部品の試験周波数である100Hzと1kHzにしか対応していませんでした。3つの方法は、それなりに相関があることがお分かりいただけると思います。
受動部品の値は特定の周波数を意識して規定されており、LCRメータはこのために複数のテスト周波数を持つことがあります。表1は、オシロスコープとファンクション・ジェネレータの組み合わせで、5つの異なる周波数での結果を示しています。テスト周波数が高くなると、テスト回路の寄生インダクタンスの影響が確認できます。テスト周波数が高くなると、測定されるキャパシタンスは小さくなります。テスト周波数の詳細については、 測定レンジ の項をご参照ください。
| Frequency | by Scope/FG | by USB VNA | by LCR | by Scope/FG | by USB VNA | by LCR |
| capacitance (μF) | capacitance (μF) | capacitance (μF) | ESR (ohm) | ESR (ohm) | ESR (ohm) | |
| 10 Hz | 10.3 | 10.4 | N/A | 28.3 | 32.8 | N/A |
| 30 Hz | 10.1 | 10.4 | N/A | 9.1 | 7.8 | N/A |
| 100 Hz | 9.8 | 10.3 | 10.22 | 2.2 | 3.2 | 2.3 |
| 300 Hz | 9.8 | 10.1 | N/A | 0.7 | 1.1 | N/A |
| 1 kHz | 9.7 | 9.8 | 9.96 | 0.3 | 0.3 | 0.21 |
表1. 例1の比較表。LCRのマニュアルでは0.05%の確度、USB VNAのマニュアルでは2%の確度と記載されている。
最良の結果を得るため、ノードA2で大きな電圧波形を得るには、精密抵抗(Rref)の値を十分に小さく保つ必要があります。また、抵抗が50Ωより大きくないと、ファンクション・ジェネレータの出力インピーダンス測定で影響を受けます。
例2:10mHインダクタ
テスト回路と手順は、例1のキャパシタのテストに使用したものとほぼ同じです。
ファンクション・ジェネレータを、10kHzの正弦波、50Ωで1Vppの振幅を出力するように設定します。(測定はハイインピーダンス・プローブで行うため、オシロスコープによる電圧測定は、この振幅のほぼ2倍になります。)信号は、基準抵抗と被測定インダクタに印加さ
れます。オシロスコープのプローブをA1とA2に接続します。
その波形を図6に示します。
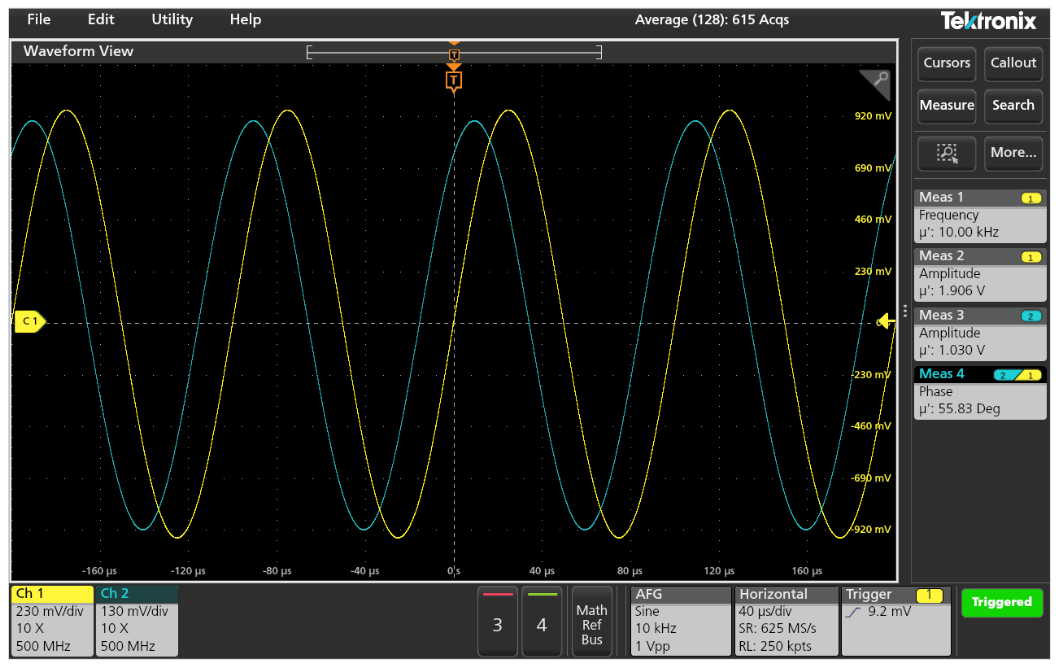
オシロスコープでアベレージ・モードを選択し、アベレージの回数を128に設定します。こうすることで、測定におけるランダム・ノイズを抑えることができます。
オシロスコープを設定して、Ch1の周波数、Ch2とCh1間の位相、Ch1の振幅、Ch2の振幅を測定します(図6参照)。これらの値を記録します。
測定のセットアップは、以下の通りです。
出力周波数、f = 10kHz
精密抵抗、Rref = 1kΩ
オシロスコープによる測定から、以下の値が得られます(図6参照)。
A1における電圧振幅、VA1 = 1.906V
A2における電圧振幅、VA2 = 1.030V
A2で測定した、A1に対する電圧の位相差、θ= 55.83°
ノードA1の電圧は試験回路全体の電圧降下、ノードA2は被測定インダクタの電圧降下になります。直列RL回路の予想通り、インダクタの電圧は回路全体の電圧に対して位相角θだけ進みます。
例1のキャパシタ測定で使用したのと同じ式で、DUTのインピーダンスを計算することができます。インピーダンスは極座標で表すことができ、その大きさと角度は次の式で求められます。

ここで、インピーダンスの直交形式に変換して、抵抗とインダクタンスを求めることができます。
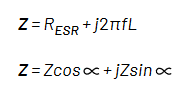
上記の式を用いて、DUTのESRとインダクタンスを求めることができます。
式 6:
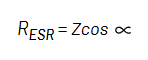
式 7:
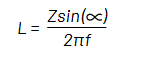
式6と式7から、被測定インダクタのESRとインダクタンスを計算することができます。

キャパシタと同様、オシロスコープとファンクション・ジェネレータで得られた結果は、LCRメータとローコストVNAによる結果に近いものでした。
テスト周波数の詳細については 測定レンジ の項をご参照ください。
最適な結果を得るため、Rrefの値は実験する必要があるかもしれません。
インダクタンスとキャパシタンスの測定レンジ
このインピーダンス測定法では、出力周波数とDUTのキャパシタまたはインダクタの値に現実的な制約があります。
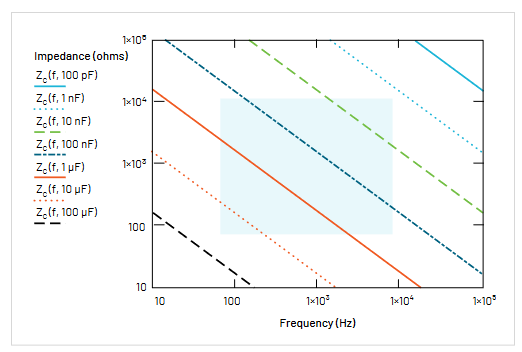
図7は、キャパシタンス/周波数とインピーダンスの関係を示しています。キャパシタンスとテスト周波数がこのボックス内に収まっていれば、測定できるはずです。色掛けされている領域では測定確度は約3%、領域外では約5%に低下します。この不確かさは、オシロスコー
プで波形を画面いっぱいに表示し、128回でアベレージングし、振幅と位相の平均値を用いて計算した場合を想定しています。
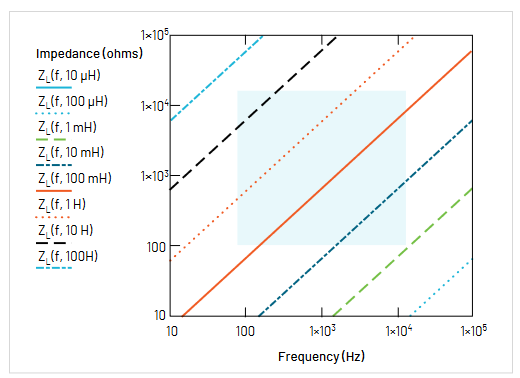
インダクタ・テストにおける同様の図を図8に示します。
まとめ|インピーダンス測定
研究室にLCRメータがない場合、または正弦波出力でキャパシタやインダクタの挙動を検証する場合、オシロスコープとファンクション・ジェネレータを使えば、簡単でわかりやすいインピーダンス測定が可能です。3~6%の不確かさでキャパシタンス、インダクタンスの値が測定できます。この方法を利用するには、十分な周波数と振幅を持ったファンクション・ジェネレータ、優れた仕様と前述の機能を備えたオシロスコープ、いくつかの精密抵抗、そして電卓表計算ソフトがあればよいのです。
詳細はテクトロニクスの 公式サイトTEK.COM/jaをご覧ください。
インピーダンス測定に対応可能な製品
インピーダンス測定に対応可能なテクトロニクス製品をご紹介します。
AFG3000Cシリーズ任意波形/ファンクション・ジェネレータ
ファンクション・ジェネレータは、クラス最高の性能で正確に信号を再生します。大型ディスプレイと25種類のショートカット・キーを備え、優れた操作性を実現しています。また標準で12種類の波形に対応し、任意波形生成機能に加え、ストレス信号のオプションもあり、1台でさまざまなアプリケーションに対応します
MDO4000シリーズ
優れた性能を備えたミックスド・ドメイン・オシロスコープ、MDO4000シリーズは、ファンクション・ジェネレータ、内蔵スペクトラム・アナライザといったオプションのほか、最大6種類の計測器の機能を備えています。他社の計測器とは異なり、RF、アナログ、デジタルのチャンネルを同期させることができるため、従来の製品にはない詳細な解析が可能です。




